River Crossings

First scenario:

How would you help a wolf, a goat, and a cabbage cross the river?

Rules:

• Your boat can hold 1 item (wolf, goat, or cabbage) plus you.
• You can’t leave the wolf and goat together, since wolves eat goats.
• You can’t leave the goat and cabbage together, since goats eat cabbages.

More to Explore:

1. What if you had more than one wolf? More than one goat? More than one cabbage
2. What if your boat could hold more than one item?
3. If you have any number of wolves, goats, and cabbages, what’s the smallest boat you need in order to help them all across the river?

Second scenario:

How would you help 1 adult and 1 child cross the river?

Rules:

• An adult weighs twice as much as a child.
• Your boat can hold two children or one adult.
• At least one adult or child needs to be in the boat to row from one side to the other.

More to Explore:

1. What if there are 3 adults and 3 children? 4 adults and 4 children? More?
2. If your boat can hold 3 children (or an equivalent weight), how does that affect your answers to the previous question? 4 children? 5? More?

Third scenario:

How would you help 2 zombies and 2 humans cross the river?

Rules:

• Your boat can hold two individuals: two zombies, two humans, or one zombie and one human.
• At least one zombie or human needs to be in the boat to row from one side to the other.
• If there are ever more zombies than humans on one side of the river (on the shore and in the boat), then the zombies will eat all of the humans.

More to Explore:

1. What if there are 4 zombies and 4 humans? 5 zombies and 5 humans? More?
2. If your boat can hold 3 individuals, how does that affect your answer to the previous question? 4 individuals? 5? More?
3. Zombie children are too weak to row the boat. If you have 3 humans, 2 zombie adults, and one zombie child, can you still help all of the zombies and humans cross the river?
4. How would your answers to question 2 change if one of the zombies is a zombie child? If two zombies are zombie children? More?

Fourth scenario:

How would you help 5 monsters cross the river?

Rules:

• Each monster has a different number of eyes: Monster 1 has 1 eye, Monster 2 has 2 eyes, Monster 3 has 3 eyes, and so on.
• Your boat can hold 2 monsters plus you.
• If left together, a monster will eat its largest proper factor. For example, the factors of 4 are 1, 2, 4 and its proper factors are 1 and 2 (as proper factors are any factors of the number that are smaller than the number itself). Therefore the largest proper factor of 4 is 2 and so Monster 4 will only eat Monster 2.

More to Explore:

1. Can you help the first 6 monsters cross the river? 7 monsters? More?
2. If your boat can hold 3 monsters, how many monsters can you help cross the river? If your boat can hold 4 monsters? 5? More?
3. You need to help 20 monsters cross the river. Can you predict how large your boat needs to be? What if you need to help 30 monsters cross the river? 40? 50? More?

• Combining story telling with preposterous scenarios (and the potential to create your own) makes for a great problem for engaging students.
• As students reason through the possible solutions, they develop their communication and logical reasoning skills.
• The activity is low-floor in that every student can get started by the simple act of trying something, yet gets progressively more difficult.
• Students are naturally pushed towards developing their own notation structures that help them strategize and discover patterns.

Why do YOU like this activity? Try it out and let us know at info@jrmf.org!

CCSS.MATH.PRACTICE.MP1
Make sense of problems and persevere in solving them.

River crossings is a low-floor problem, in that any student can get started by the simple act of trying something and seeing what happens. And then trying something else. This allows the student to focus on the mathematical process and helps develop the problem-solving skill of looking ahead, which is the ability to anticipate the results of the next few steps. From there, the students can start thinking about the solution as a pathway and think about what might hinder or help their progress. And when they successfully solve one problem, there is always another problem to challenge and engage them.

CCSS.MATH.PRACTICE.MP3
Construct viable arguments and critique the reasoning of others.

This activity is great for getting students to explain their thinking because it's framed as a story. This provides starting points for their arguments like "We need to bring the wolf, because..." or "We can't leave the cabbage, because three moves from now...", which encourages them to practice their mathematical communication skills.

CCSS.MATH.PRACTICE.MP4
Model with mathematics.

This idea of working with constraints is an important idea in mathematics and river crossing puzzles make readily apparent the need to develop an organized and readable way of representing them. This notation will vary between students but they should be encouraged to develop some kind of tracking system that makes sense to them. It will also help with logical reasoning as well as students explain their model.

CCSS.MATH.PRACTICE.MP7
Look for and make use of structure.

Tracking their moves helps here as students may recognize cases or dead ends they have already encountered. This helps them move from trial and error and into sense-making and pattern recognition. It provides the tool to help them reason through more challenging problems.

Problem History

River crossing puzzles are a genre of logic puzzles often attributed to Alcuin of York (735-804) although versions of this puzzle have been found throughout Europe and Africa. In our sequences, we have retained two of the classics - wolf/goat/cabbage and adult/child puzzles - and added two more. Zombies and Humans is our spin on the dated cannibal-missionary puzzles and Monsters is our fun, novel puzzle that adds an arithmetic aspect.

Mathematical Theory

State Transition Graphs

At the heart of every river crossing puzzle is a collection of legal arrangements (or states) and transitions from one state to another. A natural way to represent a puzzle is as a graph, taking these states as vertices and transitions as edges. In the classic wolf-goat-cabbage puzzle, there are 16 possible states, divided into legal and illegal:

Legal

Illegal

We can then examine the 10 legal states and diagram the possible transitions:

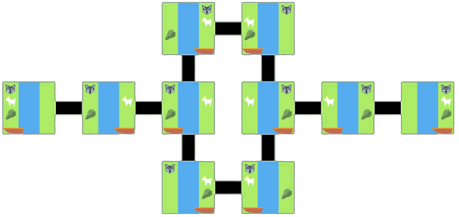
The far left vertex is the starting state and the far right is the desired end state, so solving the puzzle now amounts to finding a path from the start to end following the edges. We can see there are two shortest paths (the upper path and the lower path), each requiring 7 crossings.

Vertex Covers

In a generalized version of the wolf-goat-cabbage problem, imagine that you have a large collection of objects where each pair can either be left together unsupervised or not. If there are n objects, then the puzzle can always be solved if there are n spaces in the boat, since the ferry person can keep an eye on all of them with a single trip. However, the puzzle may not be solvable if the boat only has room for a single item. There is a smallest boat that can be used to solve the puzzle, and the number of items this boat can ferry is called the Alcuin number. By the above discussion, the Alcuin number is always between 1 and n, inclusive.

For more details on the history and theory behind River Crossings puzzles, see here!